Pour tirer le meilleur parti de nos cristaux PPLN, vous devez prendre en compte quatre aspects clés
- Longueur du cristal
- Polarisation
- Mise au point et agencement optique
- Température et période
Longueur du cristal
Chaque cristal possède une bande passante d'acceptation associée (en µm ) inversement proportionnelle à sa longueur ; cette dernière est donc unctoimportant lors du choix d'un cristal. Cette bande passante d'acceptation est due à la différence de vitesse de groupe entre les ondes interagissantes.
Pour les sources CW à bande étroite, nos cristaux les plus longs, de 20 à 40 mm, offrent le meilleur rendement. Cependant, pour les sources pulsées, un cristal long peut s'avérer contre-productif si la bande passante µm est nettement supérieure à la bande passante d'acceptance du cristal. Pour les impulsions nanosecondes, nous recommandons généralement des longueurs de 10 mm, tandis que nos cristaux les plus courts, de 0,5 à 1 mm, sont idéaux pour les systèmes à impulsions femtosecondes.
Pour la génération de second harmonique (GSH) d'impulsions femtosecondes, même si la bande passante p µm est nettement supérieure à la bande passante d'acceptation, il est possible d'obtenir un rendement de conversion élevé. Les fréquences p µm situées en dehors de la bande passante d'acceptation contribuent au rendement de conversion par génération de fréquences s µm , ce qui revient à comprimer l'impulsion p µm à large bande en une impulsion GSH à bande relativement plus étroite [1].
Polarisation
Pour accéder au coefficient non linéaire maximal du niobate de lithium µm , la lumière incidente doit être polarisée e, c'est-à-dire que sa polarisation doit être alignée avec le moment dipolaire du cristal. Ceci est réalisé en alignant l'axe de polarisation de la lumière parallèlement à l'épaisseur du cristal. Cette condition s'applique à toutes les interactions non linéaires de type I ou II, par exemple pour les systèmes de photons intriqués permettant la génération de paires de photons à polarisation orthogonale.
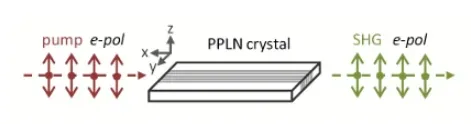
Cette configuration est connue sous le nom de correspondance de phase de type 0 (ee-e), car tous les faisceaux interagissant ont la même polarisation.
Les schémas d'accord de phase de type I (oo-e) et de type II (eo-e) sont également possibles dans le PPLN, par exemple pour la génération de photons uniques annoncés. Veuillez contacter Covesion pour discuter de vos besoins.
Mise au point et agencement optique
Les cristaux de conversion sont généralement constitués de plusieurs périodes de réseau, chacune présentant une ouverture de 0,5 × 0,5 mm² ou de 1,0 × 1,0 mm² et une longueur pouvant atteindre 40 mm. Pour obtenir un rendement de conversion élevé dans un PPLN, le faisceau p µm p doit être focalisé sur un réseau, le foyer étant centré sur la longueur du cristal.
Pour la génération de second harmonique (GSH) avec des lasers à onde continue (CW), un résultat théorique de Boyd et Kleinmann montre qu'une efficacité optimale dans le domaine µm est atteinte lorsque le rapport entre la longueur du cristal et le paramètre confocal est de 2,84 [2]. (Le paramètre confocal est le double de la distance de Rayleigh). Ceci est également valable pour les interactions de génération de fréquence somme (GFS), où les deux faisceaux π µm doivent également avoir la même distance de Rayleigh.
Pour les DFG et les OPO, une efficacité optimale µm nécessite une condition de focalisation confocale, c'est-à-dire que la portée de Rayleigh est égale à la moitié de la longueur du cristal.
Ces conditions de focalisation s'appliquent également aux lasers pulsés, mais en raison de leurs puissances de crête élevées, les exigences relatives à la taille du spot sont moins sensibles. (Attention au seuil d'endommagement du cristal afin d'éviter une focalisation trop serrée.)
En règle générale, une bonne pratique pour optimiser la taille du faisceau (en µm ) consiste à choisir une taille de spot telle que la portée de Rayleigh soit égale à la moitié de la longueur du cristal. On peut ensuite réduire la taille du spot par petits incréments jusqu'à obtenir une efficacité µm .
Température et période
La période de polarisation d'un cristal PPLN est déterminée par les longueurs d'onde de la lumière utilisée. La longueur d'onde de quasi-accord de phase peut être légèrement ajustée en modifiant la température du cristal.
La gamme de cristaux PPLN prêts à l'emploi de Covesion comprend plusieurs périodes de polarisation différentes, permettant ainsi l'utilisation de différentes longueurs d'onde à une température de cristal donnée. Nos courbes d'accord calculées indiquent précisément la température requise pour l'accord de phase. La dépendance de l'efficacité de conversion à la température suit une fonction sinc² , décrivant la bande passante d'acceptation du cristal. Plus le cristal est long, plus la bande passante d'acceptation est étroite et sensible.
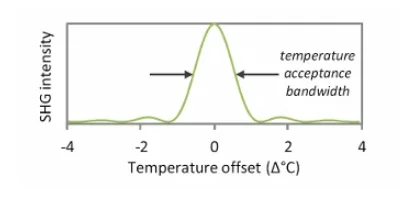
Dans de nombreux cas, l'efficacité de l'interaction non linéaire est très sensible à des variations de température inférieures à 1 °C. Par exemple, pour la génération de second harmonique (GSH) avec un couplage impulsionnel de 1064 µm dans un cristal de 20 mm de long, la bande passante de tolérance en température est d'environ 1 °C. Ainsi, si la température s'écarte de 0,5 °C de la température optimale µm couplage µm , la puissance de la GSH est réduite de moitié. Si la température du cristal peut être maintenue à la température optimale de couplage µm à ±0,1 °C près, la puissance de la GSH est stable à 2-3 % près.
La température optimale µm peut être déterminée en chauffant le cristal à 20 °C de plus que la température calculée, puis en laissant le cristal refroidir tout en surveillant la puissance de sortie à la longueur d'onde générée.
Le four Covesion PPLN s'intègre facilement dans un système optique. Associé au contrôleur de température OC1 de Covesion, il maintient la température du cristal à ±0,01 °C près, garantissant ainsi une puissance de sortie extrêmement stable.
Références
1. K. Moutzouris et al., Optics letters , vol. 31, no. 8, pp. 1148–50, (2006)
2. G. Boyd et D. Kleinman, Journal of Applied Physics , vol. 39, no. 8, p. 3597, (1968)

