Um das Beste aus unseren PPLN-Kristallen herauszuholen, sollten vier wichtige Aspekte berücksichtigen:
- Kristalllänge
- Polarisation
- Fokussierung und die optische Anordnung
- Temperatur und Periode
Kristalllänge
Jeder Kristall besitzt eine zugehörige Akzeptanzbandbreite im Bereich von µm , die umgekehrt proportional zur Länge ist. Daher ist die Kristalllänge ein wichtigerctobei der Kristallauswahl. Diese Akzeptanzbandbreite resultiert aus der Gruppenlaufzeitdifferenz zwischen den interagierenden Wellen.
Für schmalbandige CW-Quellen erzielen unsere längeren Kristalle mit 20 bis 40 mm Länge die beste Effizienz. Bei gepulsten Quellen kann ein langer Kristall jedoch negative Auswirkungen haben, wenn die p µm -Bandbreite deutlich größer ist als die Akzeptanzbandbreite des Kristalls. Für Nanosekundenpulse empfehlen wir typischerweise 10 mm lange Kristalle, während unsere kürzesten Längen von 0,5 bis 1 mm ideal für Femtosekundenpulssysteme sind.
Bei der Frequenzverdopplung (SHG) von Femtosekundenpulsen ist es möglich, eine hohe Konversionseffizienz zu erzielen, wenn die p- µm -Bandbreite deutlich größer als die Akzeptanzbandbreite ist. Die p- µm -Frequenzen außerhalb der Akzeptanzbandbreite tragen durch Frequenzerzeugung im s- µm -Bereich weiterhin zur Konversionseffizienz bei, indem sie den breitbandigen p µm -Frequenzbereich im Wesentlichen in einen relativ schmalbandigeren SHG-Puls umwandeln [1].
Polarisation
Um den höchsten nichtlinearen Koeffizienten von µm zu erreichen, muss das einfallende Licht e-polarisiert sein, d. h. die Polarisation muss mit dem Dipolmoment des Kristalls übereinstimmen. Dies wird erreicht, indem die Polarisationsachse des Lichts parallel zur Dicke des Kristalls ausgerichtet wird. Dies gilt für alle nichtlinearen Wechselwirkungen, beispielsweise für Wechselwirkungen vom Typ I oder II, etwa für verschränkte Photonensysteme zur Erzeugung orthogonal polarisierter Paare.
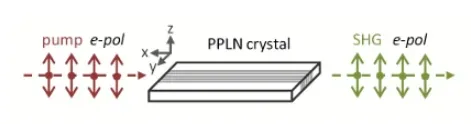
Diese Konfiguration wird als Typ-0-Phasenanpassung (ee-e) bezeichnet, da alle interagierenden Strahlen die gleiche Polarisation aufweisen.
Phasenanpassungsverfahren vom Typ I (oo-e) und Typ II (eo-e) sind auch in PPLN möglich, beispielsweise zur Erzeugung angekündigter Einzelphotonen. Bitte kontaktieren Sie Covesion, um Ihre Anforderungen zu besprechen.
Fokussierung und die optische Anordnung
Typischerweise bestehen Covesion-Kristalle aus mehreren Gitterperioden mit jeweils einer Apertur von 0,5 × 0,5 mm² oder 1,0 × 1,0 mm² und einer Länge von bis zu 40 mm. Um in PPLN eine hohe Konversionseffizienz zu erzielen, muss der p- µm -p-Strahl in ein Gitter fokussiert werden, dessen Fokus auf die Kristalllänge zentriert ist.
Für die Frequenzverdopplung (SHG) mit Dauerstrichlasern (CW) zeigt eine theoretische Berechnung von Boyd und Kleinmann, dass eine optimale µm Effizienz erreicht werden kann, wenn das Verhältnis der Kristalllänge zum konfokalen Parameter 2,84 beträgt [2]. (Der konfokale Parameter entspricht dem Doppelten der Rayleigh-Länge.) Dies gilt auch für die Summenfrequenzerzeugung (SFG), bei der die beiden p- µm -Strahlen die gleiche Rayleigh-Länge aufweisen sollten.
Für DFG und OPOs ist eine optimale µm Effizienz erforderlich, wenn die Rayleigh-Länge der konfokalen Fokussierung entspricht.
Diese Fokussierungsbedingungen gelten auch für gepulste Laser, jedoch sind die Anforderungen an die Spotgröße aufgrund der hohen Spitzenleistungen weniger empfindlich. (Beachten Sie die Zerstörschwelle des Kristalls, um eine zu enge Fokussierung zu vermeiden.)
Generell gilt für die Messung der Lichtausbeute im Bereich von µm b die Faustregel, dass die Spotgröße so gewählt werden sollte, dass die Rayleigh-Länge der halben Kristalllänge entspricht. Die Spotgröße kann dann schrittweise verringert werden, bis die maximale Lichtausbeute im Bereich µm erreicht ist.
Temperatur und Periode
Die Polungsperiode eines PPLN-Kristalls wird durch die Wellenlänge des verwendeten Lichts bestimmt. Die quasi-phasenangepasste Wellenlänge lässt sich durch Variation der Kristalltemperatur geringfügig einstellen.
Die PPLN-Kristalle von Covesion sind standardmäßig mit verschiedenen Polungsperioden erhältlich, wodurch bei einer gegebenen Kristalltemperatur unterschiedliche Wellenlängen genutzt werden können. Unsere berechneten Abstimmungskurven geben einen guten Hinweis auf die für die Phasenanpassung erforderliche Temperatur. Die Temperaturabhängigkeit des Wirkungsgrades folgt einer sinc²- Funktion , die die Akzeptanzbandbreite des Kristalls beschreibt. Je länger der Kristall, desto schmaler und empfindlicher ist die Akzeptanzbandbreite.
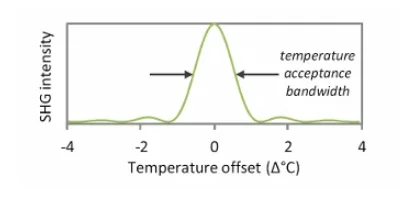
In vielen Fällen reagiert die Effizienz der nichtlinearen Wechselwirkung sehr empfindlich auf Temperaturänderungen unter 1 °C. Beispielsweise beträgt die Temperaturakzeptanzbandbreite für die Frequenzverdopplung (SHG) mit einer 1064- µm -Phasenanpassung in einem 20 mm langen Kristall etwa 1 °C. Weicht die Temperatur also um 0,5 °C von der optimalen µm ab, ist die SHG-Leistung um 50 % geringer als der optimale µm . Lässt sich die Kristalltemperatur innerhalb von ±0,1 °C auf der optimalen µm halten, ist die SHG-Leistung auf 2–3 % stabil.
Die optimale µm Temperatur kann bestimmt werden, indem man den Kristall auf 20°C über die berechnete Temperatur erhitzt und ihn dann abkühlen lässt, während man die Ausgangsleistung bei der erzeugten Wellenlänge überwacht.
Der Covesion PPLN-Ofen lässt sich problemlos in optische Aufbauten integrieren. In Kombination mit dem Covesion-Temperaturregler OC1 hält er die Kristalltemperatur auf ±0,01 °C genau und sorgt so für eine hochstabile Ausgangsleistung.
Referenzen
1. K. Moutzouris et al., Optics Letters , Bd. 31, Nr. 8, S. 1148–50, (2006)
2. G. Boyd und D. Kleinman, Journal of Applied Physics , Bd. 39, Nr. 8, S. 3597, (1968)

